He Dropped Out to Become a Poet. Now He’s Won a Fields Medal.!– OnMyWay Mobile App User News

The prize has gone to a woman for the second time in its history. One recipient didn’t start working on complex math problems until he was 23.

June Huh often finds himself lost. Every afternoon, he takes a long walk around Princeton University, where he’s a professor in the mathematics department. On this particular day in mid-May, he’s making his way through the woods around the nearby Institute for Advanced Study — “Just so you know,” he says as he considers a fork in the path ahead, “I don’t know where we are” — pausing every so often to point out the subtle movements of wildlife hiding beneath leaves or behind trees. Among the animals he spots over the next two hours of wandering are a pair of frogs, a red-crested bird, a turtle the size of a thimble, and a quick-footed fox, each given its own quiet moment of observation.

“I’m very good at finding stuff,” he says. “That’s one of my special abilities.”

Huh, 39, has now been awarded the Fields Medal, the highest honor in mathematics, for his ability to wander through mathematical landscapes and find just the right objects — objects that he then uses to get the seemingly disparate fields of geometry and combinatorics to talk to each other in new and exciting ways. Starting in graduate school, he has solved several major problems in combinatorics, forging a circuitous route by way of other branches of math to get to the heart of each proof. Every time, finding that path is akin to a “little miracle,” Huh said.

One might say the same of his path into mathematics itself: that it was characterized by much wandering and a series of small miracles. When he was younger, Huh had no desire to be a mathematician. He was indifferent to the subject, and he dropped out of high school to become a poet. It would take a chance encounter during his university years — and many moments of feeling lost — for him to find that mathematics held what he’d been looking for all along.

That poetic detour has since proved crucial to his mathematical breakthroughs. His artistry, according to his colleagues, is evident in the way he uncovers those just-right objects at the center of his work, and in the way he seeks a deeper significance in everything he does. “Mathematicians are a lot like artists in that really we’re looking for beauty,” said Federico Ardila-Mantilla, a mathematician at San Francisco State University and one of Huh’s collaborators. “But I think in his case, it’s really pronounced. And I just really like his taste. He makes beautiful things.”

“When I found out that he came to mathematics after poetry, I’m like, OK, this makes sense to me,” Ardila added.

Huh himself draws parallels between the artist and the mathematician. For both, he said, “it feels like you’re grabbing something that’s already there, rather than creating something in your mind.”

The Dropout
On any given day, Huh does about three hours of focused work. He might think about a math problem, or prepare to lecture a classroom of students, or schedule doctor’s appointments for his two sons. “Then I’m exhausted,” he said. “Doing something that’s valuable, meaningful, creative” — or a task that he doesn’t particularly want to do, like scheduling those appointments — “takes away a lot of your energy.”

To hear him tell it, he doesn’t usually have much control over what he decides to focus on in those three hours. For a few months in the spring of 2019, all he did was read. He felt an urge to revisit books he’d first encountered when he was younger — including Meditations by the Roman emperor Marcus Aurelius and several novels by the German author Hermann Hesse — so that’s what he did. “Which means I didn’t do any work,” Huh said. “So that’s kind of a problem.” (He’s since made peace with this constraint, though. “I used to try to resist … but I finally learned to give up to those temptations.” As a consequence, “I became better and better at ignoring deadlines.”)

A prime number is a whole number that possesses exactly two divisors: 1 and itself. Thus, 2, 3, and 5 are prime; 6 is not, because it can be divided by 2 and 3.

“I personally find them just totally fascinating,” said James Maynard of the University of Oxford. “They feel like some of the most basic and fundamental objects in mathematics.”

More than 2,000 years ago, Euclid proved there are an infinite number of prime numbers, but many more questions about prime numbers remain.

“It’s the tension between being somehow simple and fundamental but mysterious and poorly understood,” Dr. Maynard said. “Which is really why they fascinate me so much.”

One of the unsolved problems is the Twin Prime Conjecture. Other than 2, even numbers are not prime because all even numbers can be divided by two. Thus, other than 2 and 3, the smallest difference between two prime numbers can be 2, and such pairs, like 5 and 7 or 11 and 13, are called “twin primes.”

As numbers get larger, prime numbers become sparser. And twin primes become scarcer still — yet mathematicians had long believed there are an infinite number of twin primes.

That is, the conjecture says that for any pair of primes separated by 2, there will always be a larger pair.

That is the problem Dr. Maynard has worked on for years. “We really don’t understand the gaps between prime numbers,” he said. “Typically the gap gets pretty big as you look at bigger and bigger prime numbers.”

But occasionally, two prime numbers are relatively close to each other.

In 2013, Yitang Zhang, then a little-known mathematician at the University of New Hampshire, published a breakthrough in the problem — that there are an infinite number of prime pairs whose separation is less than 70 million. (That was an arbitrary large number where Dr. Zhang’s equations worked.)

Six months later, Dr. Maynard reproduced Dr. Zhang’s result with a different approach.

Dr. Maynard also narrowed the size of the gap to 600.

Since the ancient Greeks, mathematicians have used what is called a sieve method to find prime numbers. In the simplest version, attributed to the Eratosthenes, one can first eliminate all multiples of 2, then multiples of 3 and so on for all known primes up to a given limit.

Dr. Maynard devised an improved sieve that could find groups of primes. “It could show you that not only do you get pairs of primes coming close together, you get clusters of many primes coming close together,” he said.

Thus, he could show there were triplets of primes within a certain range as well as larger clusters.

A group of mathematicians have since collaborated to push the size of the prime gap down to 246. (That group includes Terence Tao of U.C.L.A., who won a Fields in 2006 and is one of the most influential mathematicians today. Dr. Tao came up with almost the same result as Dr. Maynard but deferred publishing his result to avoid eclipsing Dr. Maynard.)

Another result that Dr. Maynard has proved is that there are an infinite number of primes that do not have the digit 7 in them. The same proof works for any other digit too.

“Although this sounds like a bit of a curiosity, the key point is that it overcame various sorts of technical mathematical hurdles for studying the prime numbers,” Dr. Maynard said.

He said he liked these problems involving prime numbers because someone who remembers some high school math can understand them.

“But then it’s sort of fascinating for me when you have to really go deeply into very complicated and very modern math to actually prove these results,” he said.

OVERVIEW

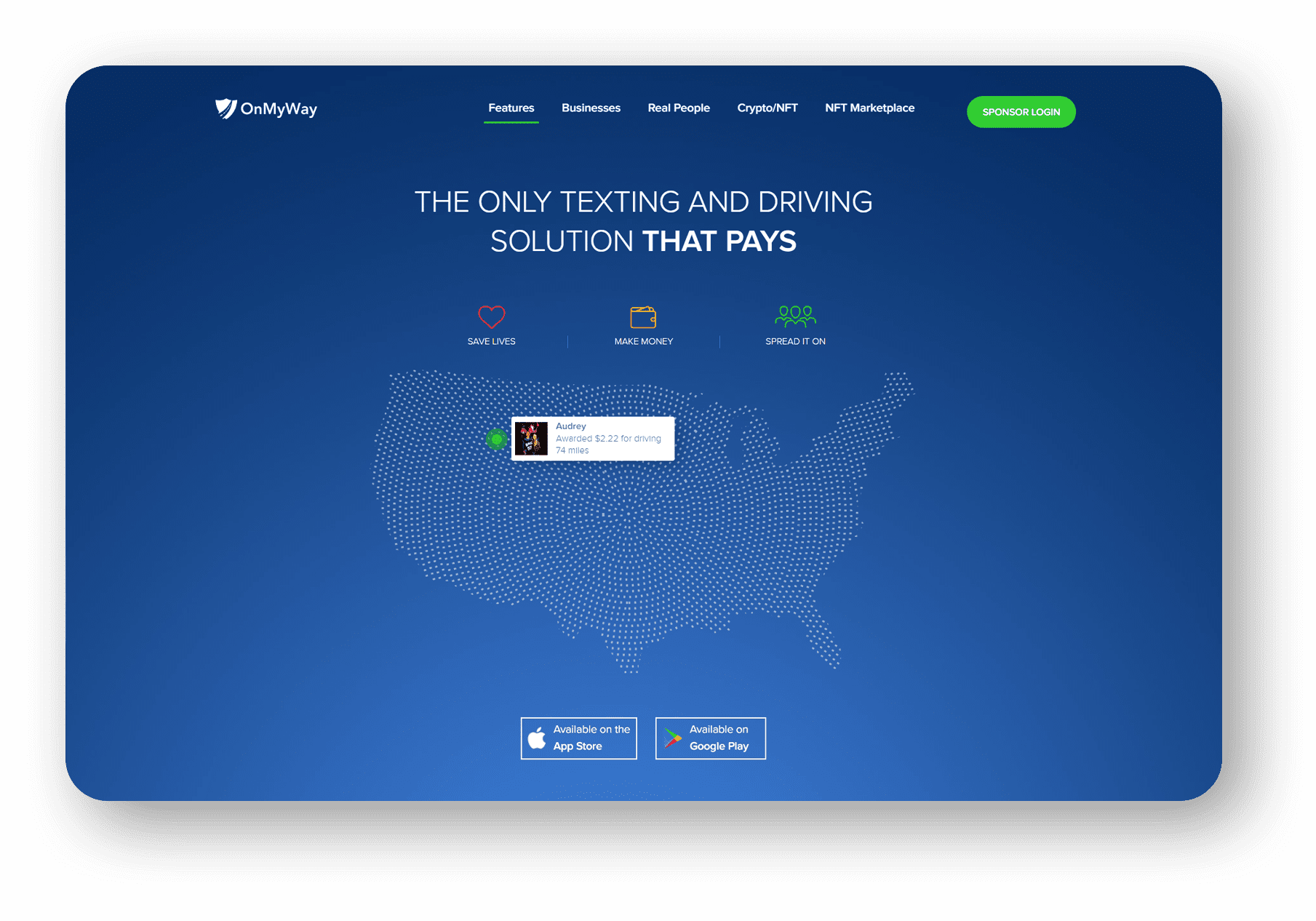
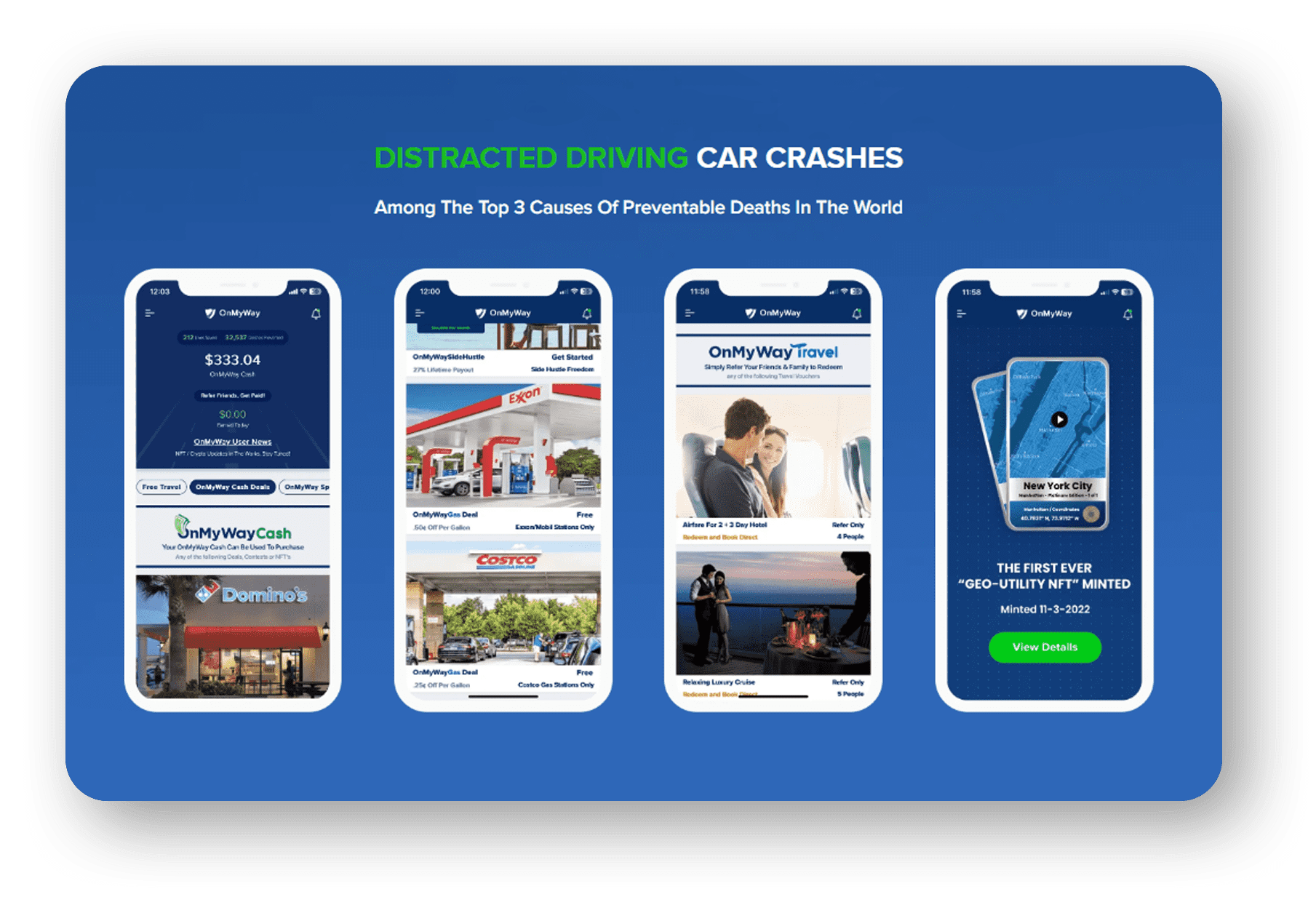
OnMyWay Is The #1 Distracted Driving Mobile App In The Nation!

OnMyWay, based in Charleston, SC, The Only Mobile App That Pays its Users Not to Text and Drive.

The #1 cause of death among young adults ages 16-27 is Car Accidents, with the majority related to Distracted Driving.

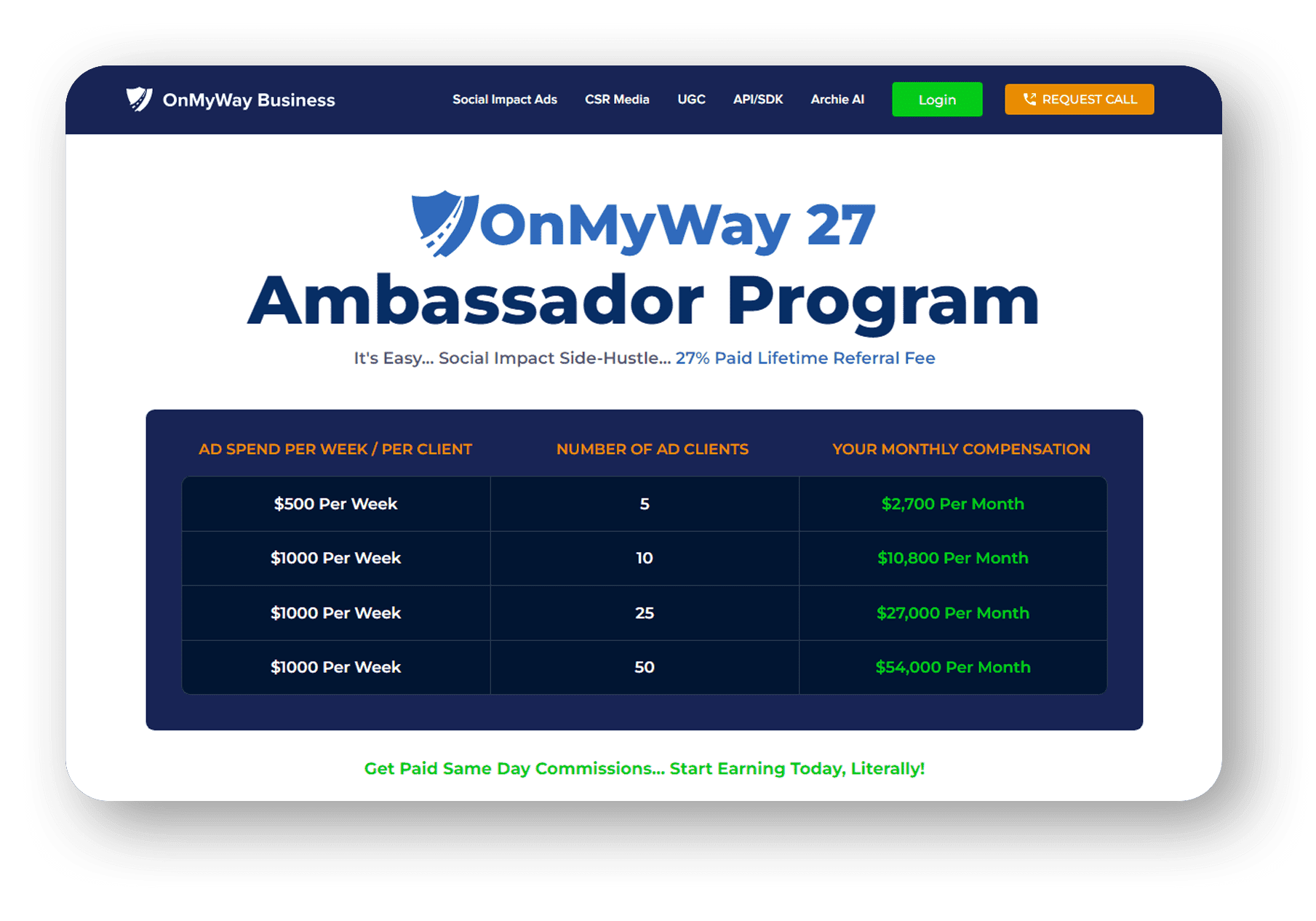
OnMyWay’s mission is to reverse this epidemic through positive rewards. Users get paid for every mile they do not text and drive and can refer their friends to get compensated for them as well.

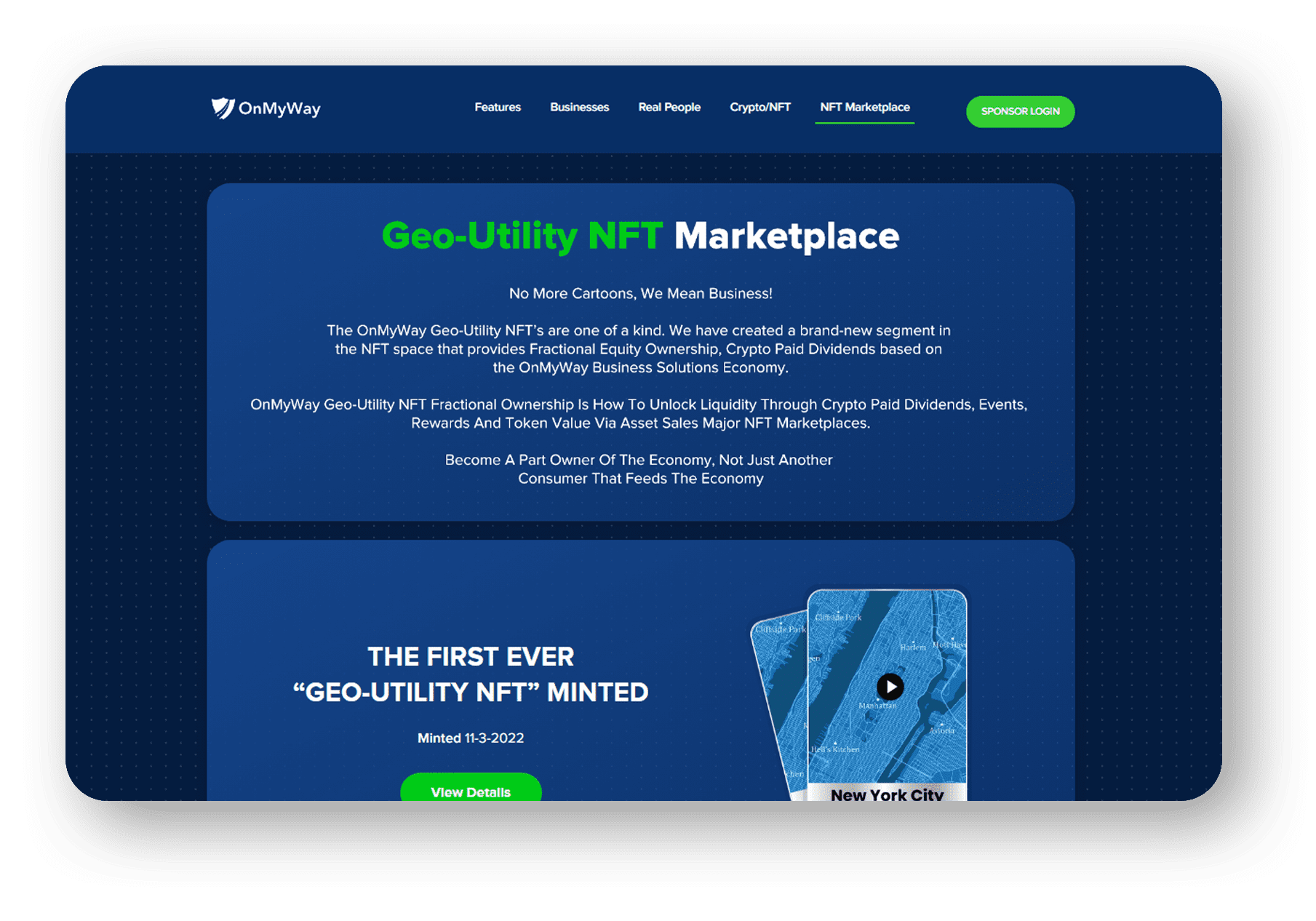
The money earned can then be used for Cash Cards, Gift Cards, Travel Deals and Much, Much More….

The company also makes it a point to let users know that OnMyWay does NOT sell users data and only tracks them for purposes of providing a better experience while using the app.

The OnMyWay app is free to download and is currently available on both the App Store for iPhones and Google Play for Android @ OnMyWay; Drive Safe, Get Paid.

Download App Now – https://r.onmyway.com

Sponsors and advertisers can contact the company directly through their website @ www.onmyway.com.